Additive Manufacturing

Additive manufacturing (AM) facilitates the fabrication of complex structures that would otherwise be difficult to make using other manufacturing methods. The spatial and dimensional errors that arise during fabrication using extrusion-based AM methods, like direct write (DW) printing, inhibit manufacturing parts with increased geometric fidelity. This research presents a method for measuring and correcting geometrical errors in DW-printed 3D periodic structures while they are fabricated. A process monitoring system is developed to measure the deposited material directly, and an iterative learning control (ILC) algorithm is implemented to compensate for the measured errors.

Process Monitoring

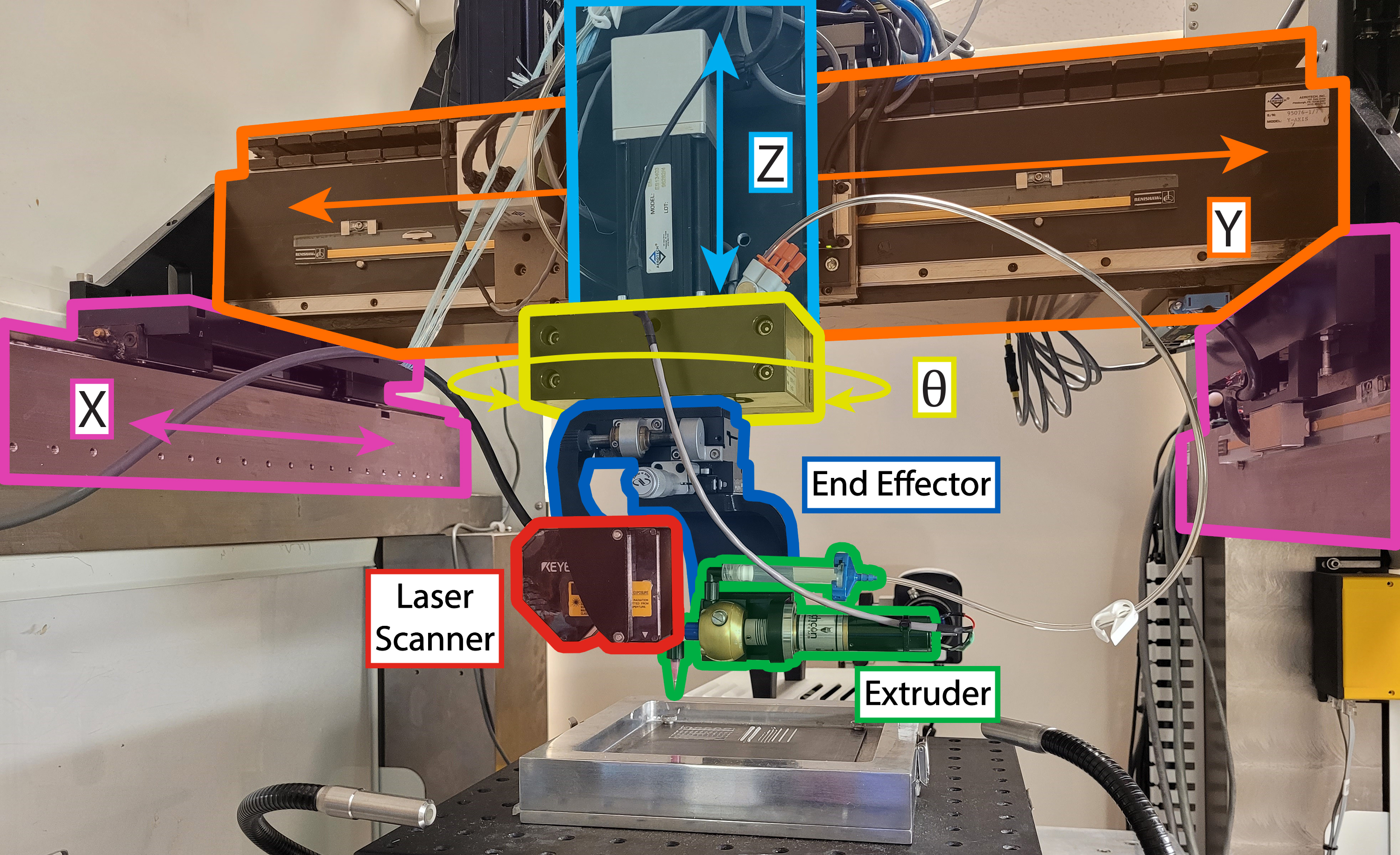
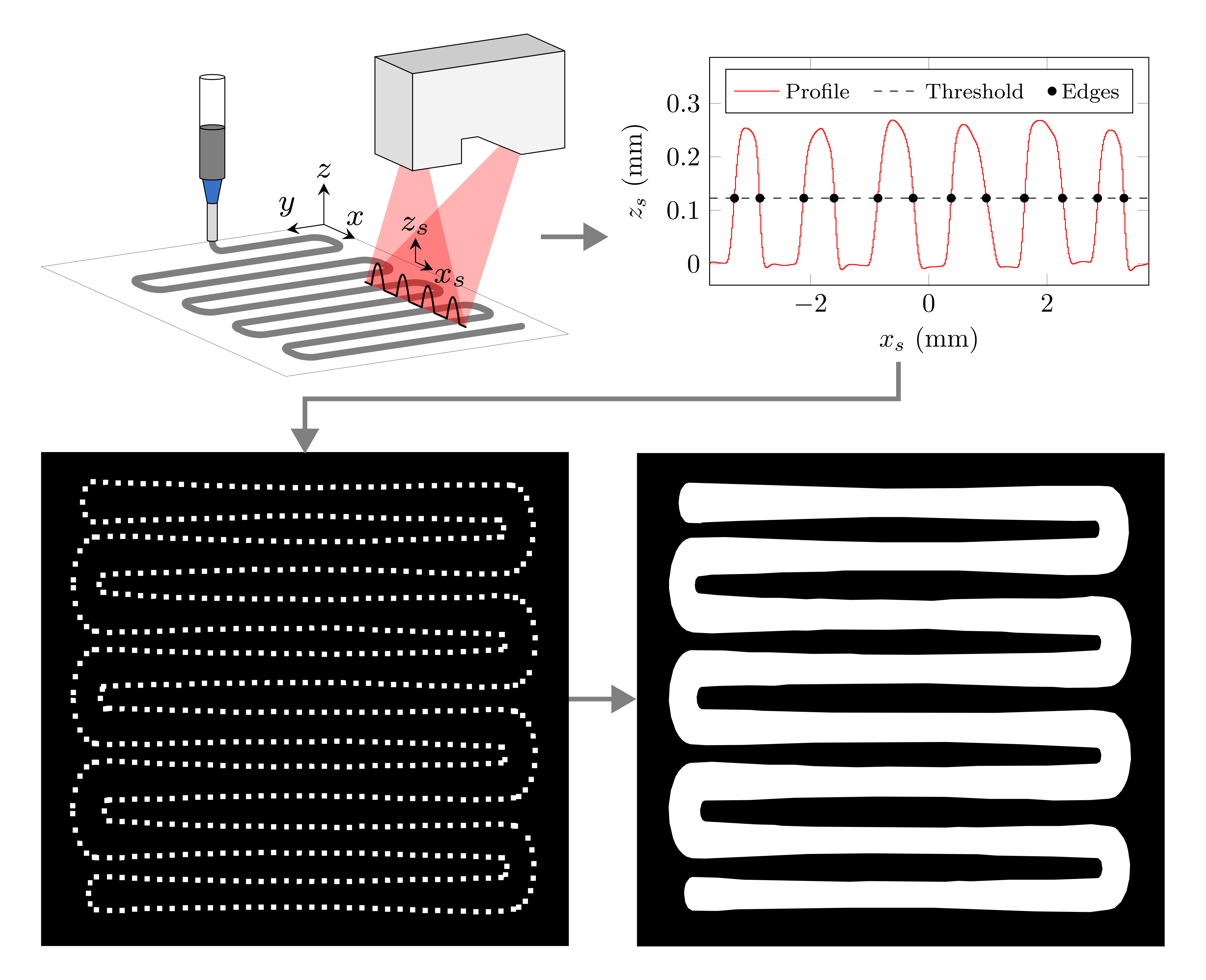
The DW printing system consists of a four-axis positioning system that moves the end effector containing the material deposition system (extruder) and process monitoring sensor (laser scanner) along a defined trajectory. As the end effector moves, the extruder deposits the material in the shape of the desired part, and the laser scanner measures the deposited material.

The DW printing system utilizes a 2D laser line scanner to take direct profile measurements of the deposited material. As the part is fabricated, the laser scanner follows a motion plan that tracks the print head’s position, generating time-delayed profile scans of the deposited material. An algorithm is developed to process the scans into a 2D projection of the structure and calculate the material’s bead width and centerline contour errors. This algorithm runs during the print, enabling the process monitoring system to determine the part’s geometric errors asynchronously, i.e., online but not in real time.

The laser scanner collects height profiles of the deposited material (top left). The edges of the material are extracted from the height profile (top right) and transformed to a global coordinate system (bottom left). The endividual edges are then stiched together to form a continuous 2D projection of the deposited material (bottom right).

Control Strategy

Iterative learning control (ILC) is a feedforward control strategy implemented on systems that perform the same task multiple times. The premise behind ILC is that system performance can be improved by learning from previous task iterations. ILC exploits trajectory repetition to generate feedforward control signals by storing the control inputs and errors of past iterations and mapping them to the current iteration control inputs.

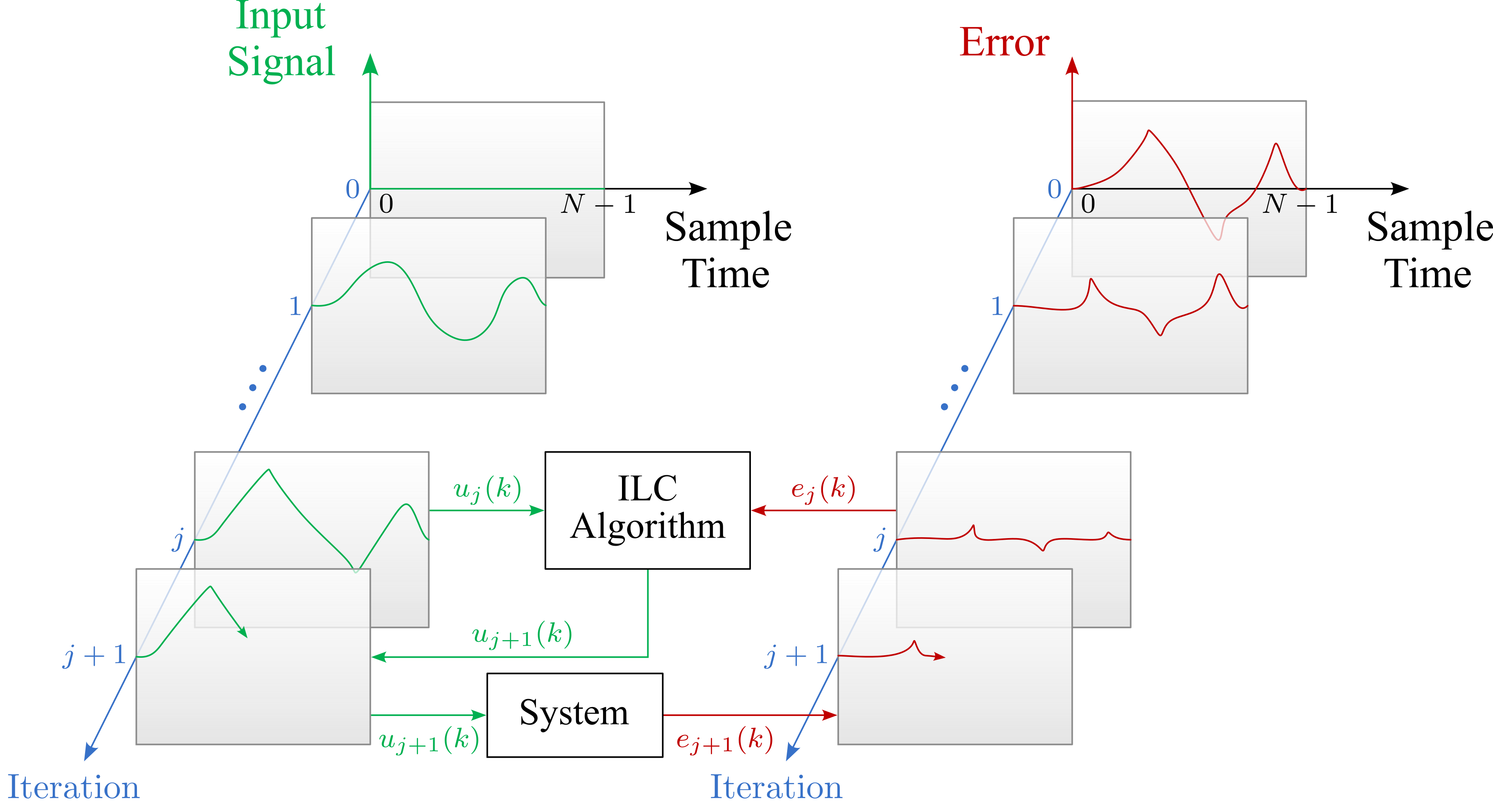
After each iteration, the previous input signal \(u_j(k)\) and the resulting error signal \(e_j(k)\) are used to calculate the updated input signal for the next iteration \(u_{j+1}(k)\).

ILC is well-suited for AM processes since they often include trajectory repetition—for example, repeating the same deposition trajectory between parts or layers. Here, the ILC algorithm learns the errors in the structure’s repetitive elements as they are printed using the online measurements, then modifies the inputs to the extrusion process to correct the errors in subsequently fabricated elements. With this implementation, the learning occurs concurrently with the printing process, which reduces the part’s errors as it prints.

The trajectory for a single layer of a scaffold structure (left) is partitioned into repeating elements (right) that are learned by the ILC algorithm as they are printed.

Experimental Validation

We experimentally validate the process monitoring and control strategy by fabricating 3D periodic lattice structures, specifically functionally graded scaffolds. The corrected prints utilizing the proposed process monitoring and control strategy show reduced errors in the material’s bead width.

Fabricating a functionally graded scaffold.
Comparison of the original uncontrolled print (left), the print corrected using the ILC algorithm (center), and the reference trajectory (right). The original scaffold appears under-extruded when compared with the reference. The initial rods (indicated by the lead-in lines) of the corrected print show similar under-extrusion; however, subsequent rods show increased material width as the inputs are learned and updated by the ILC algorithm, especially near the ends of the rods.
The root mean square (RMS) is used to quantify the bead width error of each rod segment in the printed scaffolds. After the first rods are printed (iteration 0), the ILC algorithm learns and reduces the bead width error of the subsequently printed rods (iterations 1-11).